强化学习系列(三):Model-Free Control
强化学习系列(三):Model-Free Control
Peter写在前面:系列二中提及的MC/TD方法都是在已知策略 $ \pi $ 的前提下,估计每个状态的期望回报。前者是等到整个回合结束利用完整回报 $ G_t $ 来更新价值函数,后者利用一步预测和当前奖励动态更新价值函数。可以看到的是,这些方法知识学习了价值函数,并没有改变策略。在这一节,我们主要介绍一些常用的策略优化方法。
1. Epsilon Greedy
在Model-based Control中,我们基于MDP Transition采用贪心策略进行policy improvement: $ \pi’(s)=argmax_{a \in A}R_s^a + P_{ss’}^aV(s’) $
在Model-free背景下,由于缺失MDP Transition,往往采用对行为价值函数Q(s,a)进行建模: $ \pi’(s)=argmax_{a \in A}Q(s,a) $
这里介绍一个常用的贪心策略Epsilon Greedy:
why to search bad state: 避免局部最优解,通过增加对不良状态的探索,智能体能够全面地了解环境,发现可能被忽略的潜在机会,进而提升整体策略的质量。
<定义>Greedy in the limit with infinite exploration(GLIE)
随着时间的推进,策略最终收敛到纯贪婪策略;在训练过程中,每个状态和动作都要被探索无限次,确保获得充分的信息来评估所有可能的动作。
即GLIE要求策略 $ \pi_t $ 满足以下条件:
(1) $ lim_{k->\infty}N_k(s,a)=\infty $
(2) $ lim_{k->\infty}\pi_k(a|s)=1(a=argmax_{a’ \in A}Q_k(s,a’)) $
GLIE的意义:(1)保证收敛 (2)避免局部最优
Epsilon Greedy满足GLIE:在探索的过程中逐渐减少探索率 $ \epsilon $ ,例如 $ \epsilon_t=1/t $
下面介绍下 $ \epsilon $ -Greedy与Monte-Carlo结合的Control方法:
(1) 使用当前策略 $ \pi $ 与环境进行第k次完整交互(kth episode)得到采样数据: $ \{S_1,A_1,R_2,…,,S_T\} \sim \pi $
(2) 使用MC方法对进行Q值更新: $ N(S_t,A_t) \leftarrow N(S_t,A_t) + 1 $ , $ Q(S_t, A_t) \leftarrow Q(S_t,A_t) + \frac{1}{N(S_t,A_t)}(G_t - Q(S_t, A_t)) $
(3) 基于\epsilon-Greedy进行策略提升: $ \epsilon \leftarrow 1/k $ , $ \pi \leftarrow \epsilon-greedy(Q) $
2. SARSA
将TD方法和GLIE结合的Control方法我们称其为SARSA。
下面是SARSA进行Q值更新和策略提升的伪代码:
n-step SARSA:
$ q_t^{(n)}=R_{t+1} + \gamma R_{t+2} + … + \gamma^{n-1}R_{t+n} + \gamma^n Q(S_{t+n}) $
$ Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha (q_t^{(n)}-Q(S_t,A_t)) $
3. Off-Policy Learning
on policy learning:策略学习只能使用 当前策略 生成的数据
off policy learning: 策略学习可以使用 其他策略 生成的数据,包括历史数据和经验回放
特点:训练策略和行为策略可以不同;可以使用 过去的数据(经验回放) 进行训练,提高数据利用率
对于off-policy learning,由于行为策略和训练策略并不相同,行为策略 $ \mu $ 产生的数据可能不符合目标策略 $ \pi $ 的分布,直接使用它来更新目标策略会产生偏差。为了修正分布偏差,可以采用Importance Sampling方法。
important sampling: 用于估计一个分布的期望值,而采样数据却来自另一个分布 的技术。它通过调整采样分布的影响,来修正采样偏差,使得估计值更准确。
$ E_{X\sim P}[f(X)]=\sum P(X)f(X)=\sum Q(X)\frac{P(X)}{Q(X)}f(X)=E_{X\sim Q}[\frac{P(X)}{Q(X)}f(X)] $
下面介绍Importance Sampling for Off-Policy Monte-Carlo:
Target: 通过model-free control学习一个目标策略 $ \pi $ ,但是采样数据来自于行为策略 $ \mu $
在这里,我们称 $ \mu $ 为行为策略,它负责生成训练数据; $ \pi $ 为目标策略,即我们希望学习的策略
Step:假设一个完整的episode采样序列: $ \tau = {S_1, A_1, R_2,…,S_T} $
在目标策略 $ \pi $ 中的回报期望为 $ G_t^{\pi/\mu} = \frac{\pi(A_t|S_t)}{\mu(A_t|S_t)}\frac{\pi(A_{t+1}|S_{t+1})}{\mu(A_{t+1}|S_{t+1})}…\frac{\pi(A_T|S_T)}{\mu(A_T|S_T)}G_t $
更新Q值函数: $ Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha(G_t^{\pi/\mu}-Q(S_t,A_t)) $
Ques: 为什么 $ \pi(A_t|S_t) $ 已知却不能直接用 $ \pi来更新Q值 $
Ans: 我们手头的数据是行为策略 μ 生成的,而不是目标策略 π 生成的。如果我们直接用目标策略 π 来更新Q值,实际上我们是在假设数据是按目标策略采样的,但数据实际是按行为策略采样的。这会导致估计产生偏差。
4. Q-Learning
Q-learning是一种Off-Policy Temporal Difference Learning的控制方法,它可以借助行为策略产生的数据而无需Importance Sampling
公式: $ Q(S,a) \leftarrow Q(S,a) + \alpha [R+\gamma max_{a’}Q(s’,a’)-Q(s,a)] $
Ques: 为什么Q-learning不需要重要性采样
Ans:
(1)Q-learning 的目标策略始终是贪婪策略( $ max_{a’}Q(s’,a’) $ ),但行为策略可以是探索性的(比如 ϵ-greedy)。因为它只用目标策略来选择下一个状态的最优动作,不需要纠正行为策略带来的偏差。
(2)它用的是单步TD更新,不是完整回报。TD更新只依赖当前经验(s,a,r,s’),所以行为策略只需要提供足够多样的数据,不要求它和目标策略一致
Ans:无法与真实环境交互,如何训练目标策略
Ques: Simulator和Batch RL
Simulator: 强化学习中的一个环境,允许Agent在其中交互、收集数据并进行训练。适用于Online RL(在线强化学习):算法可以随时与环境交互并收集数据(如 DQN、PPO)。
Batch RL:它仅使用一个固定的数据集来训练,而不会与环境交互。需要 Off-Policy 方法:由于数据可能来自多个不同的策略(而非当前策略),必须使用 Off-Policy RL(如 DQN、BCQ)
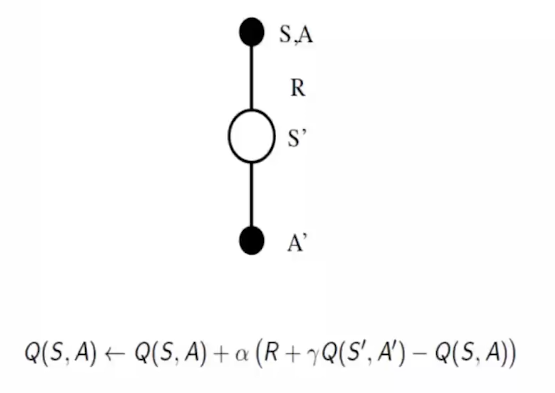
区分Q-learning和SARSA的Q值更新:
SARSA的Q值更新公式为: $ Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha[R_{t+1}+\gamma Q(S_{t+1},A_{t+1})-Q(S_t,A_t)] $
Q-learning用的是下一状态的最优动作 $ max_{a’}Q(s’,a’) $ 来更新,属于Off-Policy。SARSA用的是实际选到的下一动作 $ A_{t+1} $ 来更新,属于On-Policy。
下面给出Q-Learning的伪代码: