强化学习系列（五）：Policy Gradient

写在前面：前面所提到的Q-value Based方法无法解决连续动作空间场景下的优化问题，因为Q-learning的策略是从多个离散动作中贪婪地选择最大Q值，在连续空间中，无法枚举所有动作。为此，本节讲述一种直接面向策略的优化方法：Policy Gradient

1. Policy Gradient

训练目标： $ \pi_\theta(s,a)=P[a|s,\theta] $
Ques: 什么样的策略算是好的策略,如何进行梯度更新
Ans:
think $ \theta $ 会影响策略 $ \pi $ , $ \pi $ 会影响episode采样路径 $ \tau={s_1,a_1,r_1,s_2,a_2,r_2,…,s_T,a_T,r_T} $ ，根据 $ \tau $ , 我们可以算出 $ R(\tau)=\sum_{n=1}^N r_n $ ，我们希望采样路径的 $ R(\tau) $ 尽可能的大
method
用采样路径的平均收益来评价一个 $ \theta $ 的好坏
$ \bar R_\theta = \sum_{\tau} R(\tau) \cdot P(\tau|\theta) \approx \frac{1}{N} \sum_{n=1}^{N} R(\tau^n) $
推导 $ \bar R_\theta $ 的梯度:
$ $ \nabla \bar R_\theta=\sum_\tau R(\tau) \nabla P(\tau|\theta)=\sum_\tau R(\tau)P(\tau|\theta) \frac{\nabla P(\tau|\theta)}{P(\tau|\theta)}=
\sum_\tau R(\tau)P(\tau|\theta)\nabla logP(\tau|\theta) \approx \frac{1}{N}\sum_{n=1}^N R(\tau^n) \nabla log P(\tau^n|\theta) $ $
其中， $ P(\tau|\theta)=p(s_1)p(a_1|s_1,\theta)p(r_1,s_2|s_1,a_1)p(a_2|s_2,\theta)… $
由此，我们有： $ log P(\tau|\theta)=logp(s_1)+\sum_{t=1}^Tlogp(a_t|s_t,\theta)+logp(r_t,s_{t+1}|s_t,a_t) $
$ \nabla logP(\tau|\theta)=\sum_{t=1}^T\nabla logp(a_t|s_t, \theta) $
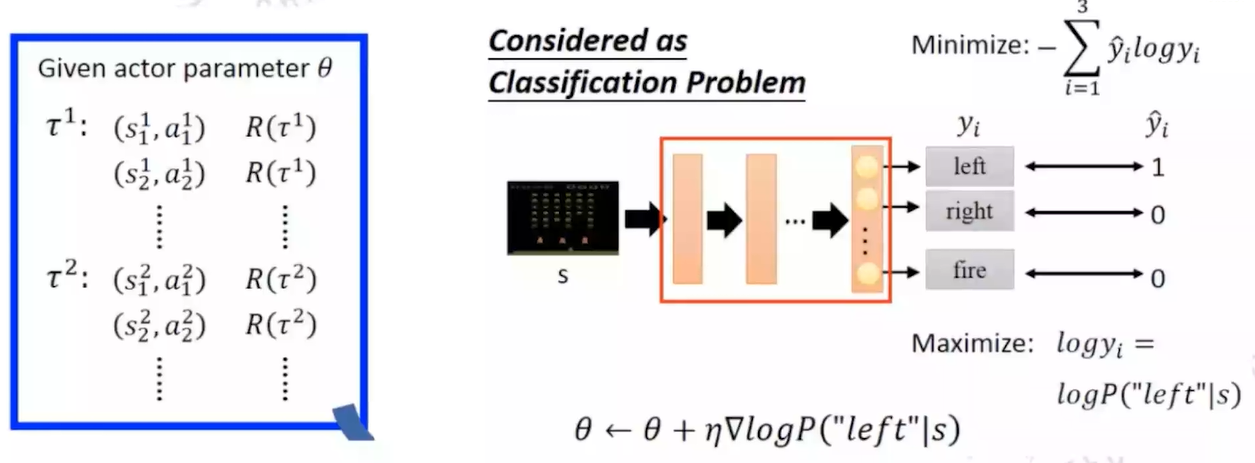
由此，我们可以将policy gradient视为一个分类任务对 $ \nabla \bar R_\theta $ 进行更新

类比分类任务：

2. Actor-Critic

在Policy Gradient方法中，我们在更新 $ \nabla \bar R_\theta $ 时，借助累计收益 $ R(\tau^n) $ 作为优势估计，然而在一些情况下，虽然 $ R(\tau^n) $ 是positive的，但是效益还比不过随机效益的话，其实也是不能接受的。因此，需要add a baseline去进一步评估positive or negtive，从而更好地指导 $ \nabla logP(\tau|\theta) $ 的更新

核心思想：
（1）Actor:学习策略 $ \pi_\theta(a|s) $ ，负责决策
（2）Critic:学习一个价值函数 $ V_w(s) $ ，估计状态的“好坏”，指导 Actor 改进策略

梯度更新：
$ $ \nabla \bar R_\theta \approx \frac{1}{N}\sum_{n=1}^{N}\sum_{t=1}^{T_n}(R_\tau^n-baseline) \nabla log P_\theta(a_t^n|s_t^n) $ $
其中 $ R_\tau^n $ 可以表示为 $ E[G_t^n]=Q^{\pi_\theta}(s_t^n,a_t^n) $ ，baseline表示为 $ V^{\pi_\theta}(s_t^n) $

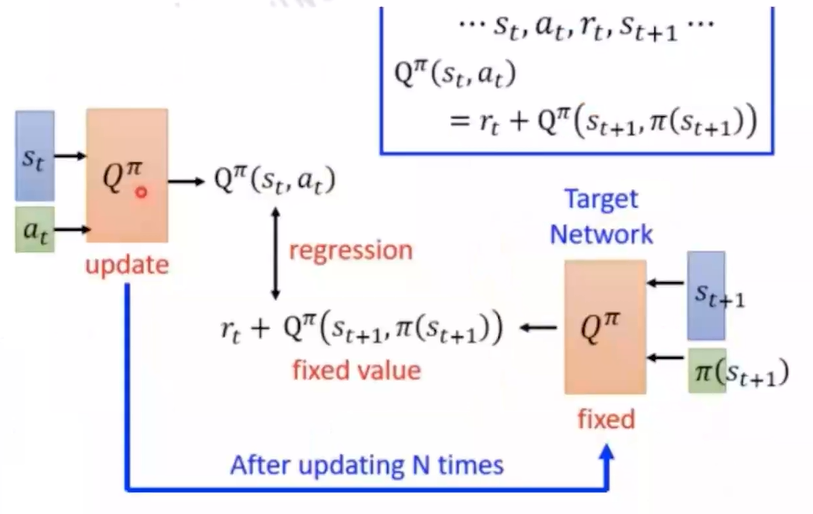
Ques: 需要estimate Q和V两个网络吗
Ans: 可以只estimate value network
利用 $ Q^{\pi_\theta}(s_t^n,a_t^n)=E[r_t^n + V^{\pi_\theta}(s_{t+1}^n)] \approx r_t^n + V^{\pi_\theta}(s_{t+1}^n) $
我们可以得到Advantage Function： $ Q^{\pi_\theta}(s_t^n,a_t^n)-V^{\pi_\theta}(s_t^n)=r_t^n - (V^{\pi_\theta}(s_t^n)-V^{\pi_\theta}(s_{t+1}^n)) $

summary