RLHF(一)：LLM post-training

Peter2025-04-172025-06-23

1. PPO算法

$ L_{PPO} = \sum_{(s_t,a_t)}\frac{\pi_\theta(a_t|s_t)}{\pi_{ref}(a_t|s_t)}A(s_t,a_t) - \beta KL(\pi_\theta, \pi_{ref}) $

PPO的训练步骤如下：
（1）收集人类反馈，人工标注数据（2）训练奖励模型（3）采用PPO强化学习，优化策略
PPO训练流程

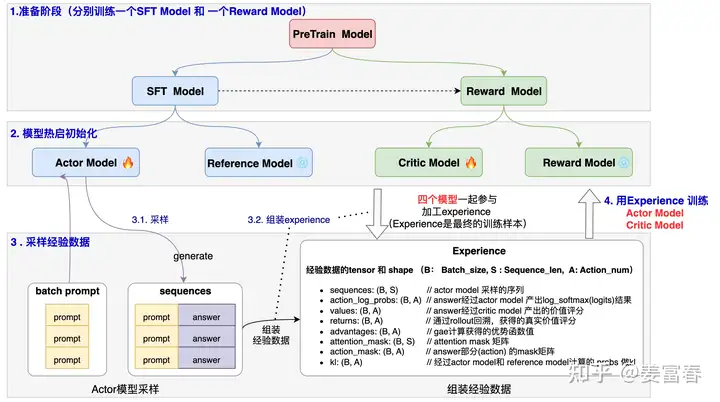
在LLM上使用PPO算法进行post-training时，主要涉及4个model:

Actor Model：是我们要优化学习的策略模型，同时用于做数据采样，用SFT Model热启
Reference Model：是为了控制Actor模型学习的分布与原始模型的分布相差不会太远的参考模型，通过loss中增加KL项，来达到这个效果。训练过程中该模型不更新
Critic Model：是对每个状态做打分的价值模型，衡量当前token到生成结束的整体价值打分，一般可用Reward Model热启
Reward Model：对整个生成的结果打分，是事先训练好的Reward Model。训练过程中该模型不更新

2. DPO算法

$ L_{DPO}(\pi_\theta; \pi_{ref}) = -E_{(x,y_w,y_l)\sim D}[log \sigma(\beta log\frac{\pi_\theta(y_w|x)}{\pi_{ref}(y_w|x)} - \beta log\frac{\pi_\theta(y_l|x)}{\pi_{ref}(y_l|x)})] $
DPO相比于PPO算法，由于它直接定义偏好损失作为策略来优化LLM，省去了奖励模型的定义，因此在post-training的流程上更为简练(PPO: SFT->RM->PPO)

如何理解DPO loss:
开始训练时，Reference model和Policy model都是同一个模型，在训练过程中Reference model不更新权重。我们将loss公式中的log部分展开，然后设 $ \beta $ 为1，并且暂时不看前面的log_sigmoid。从而将优化函数简化为： $ [logp(y_w) - logp_{ref}(y_w)]-[logp(y_l)-logp_{ref}(y_l)] $

训练的目标为将优化函数最大化。即我们希望公式的左半部分和右半部分的margin越大越好，左半部分的含义是good response相较于没训练之前的累计概率差值，右半部分代表bad response相较于没训练之前的累计概率差值

3. KTO算法

DPO算法中依赖的训练数据为：问题——期望回答——拒绝回答。高质量的偏好数据收集较为困难。KTO则回避了这个问题，可以直接利用二元信号标记的数据来训练算法，对于负样本更加敏感

前景价值函数：决策者根据实际收益或损失所产生的主观感受的价值。（决策时，相对于收益，决策者对损失更加敏感）

$v(z,z_{ref};\lambda,a) = \begin{cases} (z - z_{ref})^\alpha & \text{if } z > z_{ref} \\ -\lambda(z_{ref} - z)^\alpha & \text{if } z < z_{ref} \end{cases}$

KTO算法的loss如下：
$ L_{KTO}(\pi_\theta; \pi_{ref}) = E_{(x,y)\sim D}[\lambda_y - v(x,y)] $

$v(x,y)= \begin{cases} \lambda_D \sigma(\beta(r_\theta(x,y)-z_0)) & if y \sim y_{desirable}|x \\ -\lambda_U \sigma(\beta(z_0 - r_\theta(x,y))) & if y \sim y_{undesirable}|x \end{cases}$

其中， $ z_0 = KL(\pi_\theta(y’|x)||\pi_{ref}(y’|x)) $ ， $ r_\theta(x,y)=log \frac{\pi_\theta(y|x)}{\pi_{ref}(y|x)} $

4.GRPO算法

在PPO算法中，每个时间步都有一个价值网络去估计优势函数，这使得训练资源消耗巨大。为了减少在post-training的过程中对价值网络的依赖，GRPO采用“分组输出相互比较”的方式来估计基线，从而省去Critic Model。
关键点：分组采样与相对奖励
对于一个问题q，Actor Model会产生多份输出 $ o_1,o_2,…,o_G $ ，然后将这组输出一起送入奖励模型，得到奖励集合 $ r_1,r_2,…,r_G $ 。然后对奖励集合进行归一化 $ \tilde{r_i}=(r_i-mean(r))/std(r) $ ，从而得到分组内的相对水平，即相对奖励。GRPO会将相对奖励赋给该输出对应的所有token的优势函数。即 $ \hat{A}_{i,t} = \tilde{r_i} $ ，也就是说，输出 $ o_i $ 的所有token共享同一个分数，于是我们得到了一个无价值网络的优势函数。

综上所述，因为不再需要在每个token上拟合一个价值函数，GRPO可以大幅节省内存。

下面给出GRPO的loss function:
$ L_{GRPO}= E[\frac{1}{G}\sum_{i=1}^G \frac{1}{||o_i||}\sum_{t=1}^{||o_i||} min(\frac{\pi_\theta(o_{i,t}|q,o_{i,<t})}{\pi_{ref}(o_{i,t}|q,o_{i,<t})},clip(\frac{\pi_\theta(o_{i,t}|q,o_{i,<t})}{\pi_{ref}(o_{i,t}|q,o_{i,<t})},1-\epsilon,1+\epsilon)) \cdot \hat{A_{i,t}} -\beta KL(\pi_\theta, \pi_{ref})] $
GRPO vs PPO